算法学习笔记（六）堆结构

发表于 | 更新于 | 分类于 | 阅读次数：
本文字数： 7.8k | 阅读时长 ≈ 7 分钟
介绍堆结构，大根堆，小根堆等相关概念；堆结构的heapInsert 和 heapify操作；Java中的优先级队列（PriorityQueue）；堆排序以及扩展题目。

（一）相关概念

堆结构： 数组实现的完全二叉树结构。

满二叉树：每一层的节点都达到最大值的二叉树。

完全二叉树：满二叉树一定是完全二叉树，除了满二叉树之外，完全二叉树还包括最后一层从左到右逐渐变满而其他上面各层节点达到最大值的情况。

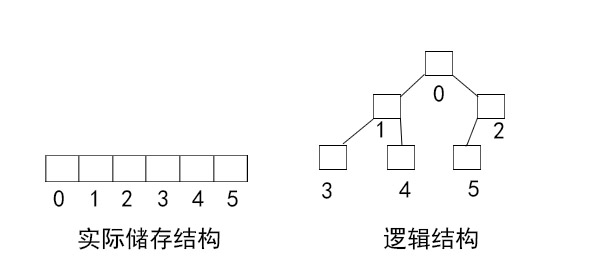
在位置i上，如有左子节点，它的左子节点的下标为2×i+1，如有右子节点，右子节点下标为2×i+2，父节点的下标为(i-1)/2。可以用这三个公式帮助想象逻辑结构。

大根堆，小根堆：完全二叉树中每个子树的最大值（最小值）是头节点的值（可以相等），那么就称作大根堆（小根堆）。

（二）堆结构的heapInsert 和 heapify操作：

假设有一个数组，当用户没有给出数时，堆上无节点，heapsize（用来控制堆的大小）= 0。用户不断给出数，要求将数放入堆并且保证一直是大根堆。那么思路就是与父节点比较，如果比父节点大就交换位置，如果小于等于父节点或者不存在父节点，就不再移动。这样的向上调整的过程就是堆结构的heapInsert。

Java

1
2
3
4
5
6
7
8
9
10
11
12
13
public static void heapInsert(int[] arr, int index) {
        // 停止条件：不比父节点位置的数大或者已经到达最头节点
        while(arr[index] > arr[(index-1)/2]) {
            swap(arr, index, (index-1)/2);
            index = (index - 1) / 2;
        }
    }
    
    public static void swap(int[] arr, int i, int j) {
        int tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }

JavaScript

1
2
3
4
5
6
7
8
function heapInsert(arr, index){
     while(arr[index] > arr[Math.floor((index-1)/2)]){
       var tmp = arr[index];
       arr[index] = arr[Math.floor((index-1)/2)];
       arr[Math.floor((index-1)/2)] = tmp;
       index = Math.floor((index - 1) / 2);
     }
   }

由于二叉树的高度的级别是logN，所以每一步的调整代价是logN，整体的时间复杂度就是O(N×logN)。

假如用户增加需求，一共n个数，新数进来，找出并移除最大值，并且让剩下的数还是大根堆。那么思路就变成将新数放在0位置上，heapsize - 1, 当0位置上的数比子节点位置数小时，就向下调整。并注意越界情况，也就是不存在子节点的情况。这种向下调整的操作就是heapify。

Java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
public static void heapify(int[]arr, int index, int size) {
        // 左孩子的下标
        int left = index*2 + 1;
        // 当存在子节点时
        while(left < size) {
            // 左孩子和右孩子的较大值下标存入largest
            int largest = left + 1<size && arr[left+1]>arr[left] ? left+1 : left;
            // 左孩子，右孩子，自身比较的最大值的下标存入largest
            largest = arr[largest]>arr[index] ? largest : index;
            if(largest == index) {
                break;
            }else {
                swap(arr, largest, index);
                index = largest;
                left = index * 2 + 1;
            }
        }
    }
    
    public static void swap(int[]arr, int i, int j) {
        int tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }

JavaScript

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
function heapify(arr, index, size){
    var left = index * 2 + 1;
    while(left < size){
      var largest = left+1<size&&arr[left+1]>arr[left] ? left+1 : left;
      largest = arr[largest]>arr[index] ? largest : index;
      if(largest == index){
        break;
      }else{
        var tmp = arr[index];
        arr[index] = arr[largest];
        arr[largest] = tmp;
        index = largest;
        left = index * 2 + 1;
      }
    }
  }

（三）Java中的优先级队列

Java中的PriorityQueue(优先级队列)的底层就是堆结构，当位置不够时会自动扩容。系统默认是小根堆。PriorityQueue会根据排序规则决定哪个元素在队首，哪个在队尾。

Java中PriorityQueue基本操作：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import java.util.PriorityQueue;

public class Test {
    public static void main(String[] args) {
        PriorityQueue<Integer> heap = new PriorityQueue<Integer>();
        // 向队列中加入数据, add()和offer()均可
        heap.add(6);
        heap.add(4);
        heap.add(8);
        heap.add(7);
        while(!heap.isEmpty()) {
            // 获取最大值并移除
            System.out.println(heap.poll());// 4 6 7 8
            // 如果不移除，用peek()方法
        }
    }
}

（四）堆排序

堆排序可以分为以下几个步骤：

  1. 让整个数组变成大根堆，建立堆的过程：可以用heapInsert或heapify方法，如果用前者，则时间复杂度为O(N×logN)，如果用heapify的时间复杂度为O(N)。如何得出向下比较的heapify方法（从下往上建堆）的时间复杂度时O(N)呢？先假设完全二叉树共有n个节点，并且假设是满二叉树（满二叉树时性能最差）。那么最后一层有n/2个节点，它们不需要向下比较，因此最后一层的常数操作数为n/2；倒数第二层n/4个节点，除了看自己之外还可能需要向下调整，调整的距离为1，因此每个数最多两次常数操作，n/4×2，保证了最后一层和倒数第二层构成大根堆结构；倒数第三层n/8节点，调整距离为2，每个数最多三次常数操作，n/8×3；以此类推，T(n) = n/2 + n/4×2 + n/8×3 + …… 等式两边同时乘2得到的式子与T(n)错位相减，得出时间复杂度O(N)。

  2. 将堆的最大值和最末尾的值交换，然后heapsize-1，代表排在末尾的最大值与堆断连。再将堆调整成大根堆。

  3. 当heapsize值为0时，整体排序完成。

    虽然第一个步骤通过heapify可以将时间复杂度降至O(N)，但第二个步骤的时间复杂度无法改变，因此整个堆排序的时间复杂度为O(N×logN)，过程中用了有限几个变量，所以额外空间复杂度为O(1)。

Java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
public class Test {
    
    public static void heapSort(int[] arr) {
        if(arr.length<2 || arr==null) {
            return;
        }
        int heapsize = arr.length;
        // 让整个数组变成大根堆
        for(int i=heapsize-1; i>=0; i--) {
            heapify(arr, i, heapsize);
        }
        // 大根堆的最头节点和最后一个值交换，并将其断联
        swap(arr, 0, --heapsize);
        // 直到heapsize为0时，整个排序完成
        while(heapsize > 0) {
            heapify(arr, 0, heapsize);
            swap(arr, 0, --heapsize);
        }
    }
    
    public static void heapify(int[] arr, int index, int size) {
        int left = index * 2 + 1;
        while(left < size) {
            int largest = left+1<size&&arr[left+1]>arr[left] ? left+1 : left;
            largest = arr[largest]>arr[index] ? largest : index;
            if(largest == index) {
                break;
            }
            swap(arr, largest, index);
            index = largest;
            left = index * 2 + 1;
        }
    }
    
    public static void swap(int[] arr, int i, int j) {
        int tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }
    
    public static void main(String[] args) {
        int[] arr = {2,3,9,5,8,7,1};
        heapSort(arr);
        for(int i=0; i<arr.length; i++) {
            System.out.println(arr[i]);// 1 2 3 5 7 8 9
        }
    }
}

JavaScript

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
var arr = [2,3,9,5,8,7,1];
heapSort(arr);
console.log(arr);

function heapSort(arr){
  if(arr.length<2 || arr==null){
    return;
  }
  var heapsize = arr.length;
  for(var i=heapsize-1; i>=0; i--){
    heapify(arr, i, heapsize);
  }
  swap(arr, 0, --heapsize);
  while(heapsize > 0){
    heapify(arr, 0, heapsize);
    swap(arr, 0, --heapsize);
  }
}

function swap(arr, i, j){
  var tmp = arr[i];
  arr[i] = arr[j];
  arr[j] = tmp;
}

function heapify(arr, index, size){
  var left = index * 2 + 1;
  while(left < size){
    var largest = left+1<size&&arr[left+1]>arr[left] ? left+1 : left;
    largest = arr[largest]>arr[index] ? largest : index;
    if(largest == index){
      break;
    }else{
      var tmp = arr[index];
      arr[index] = arr[largest];
      arr[largest] = tmp;
      index = largest;
      left = index * 2 + 1;
    }
  }
}

（五）堆排序扩展题目

已知一个几乎有序的数组，几乎有序指的是如果把数组排好顺序之后，每个元素移动的距离不超过k，并且k对于数组来说比较小。要求选择合适的排序算法对数组进行排序。

堆排序是解决这个问题的好方法，假如k的值为5，那么可以让前6个数进入小根堆，最小值放在0位置，移除再加入新数（也可以5个数进入小根堆，区别在于这样需要向加入新数，再弹出堆）。小根堆记录维持了所有可能性。此过程的时间复杂度为O(N×logk)，当k很小时，效率很高。具体代码如下：

Java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
import java.util.PriorityQueue;

public class Test {
    
    public static void sortArrayLessK(int[] arr, int k) {
        PriorityQueue<Integer> heap = new PriorityQueue<>();
        // 将前k个数加入堆中，注意数组长度与k的关系
        int index = 0;
        for(;index<Math.min(arr.length, k); index++) {
            heap.add(arr[index]);
        }
        // 堆中依次加入数组中后面的数，并弹出距离超过k的数，因为不在考虑范围
        int i=0;
        for(; index<arr.length; i++, index++) {
            heap.add(arr[index]);
            // 弹出的数记录在数组中
            arr[i] = heap.poll();
        }
        // 将堆中最后剩余的数加入数组中
        while(!heap.isEmpty()) {
            arr[i++] = heap.poll();
        }
    }
    
    public static void main(String[] args) {
        int[] arr = {1,5,3,4,6,2};
        sortArrayLessK(arr,5);
        for(int i=0; i<arr.length; i++) {
            System.out.println(arr[i]);// 1 2 3 4 5 6
        }
    }
}